 |
||||||||||||||||||||||||||||||||||||
|
1. Vectors and scalars
|
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
A vector is a quantity with magnitude and a direction. The magnitude of the vector is also called its length. Examples: velocity, acceleration, momentum, force, electric and magnetic field intensities. A vector is represented by a directed line segment. The direction of the vector is indicated by an arrow pointing from the tail to the head. If the tail is at point A and the head is at point B, the vector from A to B is written
The length (magnitude) of a vector v is written |v|. The length is always a non-negative real number.
For example, we can draw a vector from corner A of a house to corner B. The vector
You get the same vector if you start at some other point C and then draw
an arrow in the same direction as All that matters is the direction and magnitude of the vector; if these stay the same we are looking at the same vector, no matter where it appears. For an illustration, click the button below. The arrow moves but its direction and length remain the same, therefore it always represents the same vector.  
Copyright © 2003 The University of Sydney
|
|||||||||||||||||||||||||||||||||||
| Feedback |
|
|||||||||||||||||||||||||||||||||||
© 2002-09 The University of Sydney. Last updated: 09 November 2009
ABN: 15 211 513 464. CRICOS number: 00026A. Phone: +61 2 9351 2222.
Authorised by: Head, School of Mathematics and Statistics.
Contact the University | Disclaimer | Privacy | Accessibility
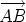 .
.
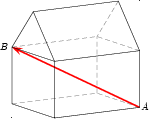
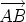 has direction and length but exists independently of the house.
has direction and length but exists independently of the house.
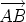 and with the same length as that of
and with the same length as that of
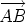 .
.