 |
||||||||||||||||||||||||||||||||||||
|
1. Vectors and scalars
|
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
Even though we have said that all vectors have length and direction, there is one exception: the zero vector. The zero vector 0 is the vector from a point A to the same point A. We can write
0 = The zero vector does not have a direction but it does have a length; not surprisingly, its length is 0. Thus we can write |0| = 0.
Copyright © 2003 The University of Sydney
|
|||||||||||||||||||||||||||||||||||
| Feedback |
|
|||||||||||||||||||||||||||||||||||
© 2002-09 The University of Sydney. Last updated: 09 November 2009
ABN: 15 211 513 464. CRICOS number: 00026A. Phone: +61 2 9351 2222.
Authorised by: Head, School of Mathematics and Statistics.
Contact the University | Disclaimer | Privacy | Accessibility
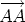 no matter where the point
no matter where the point