 |
||||||||||||||||||||||||||||||||||||||||||
|
12. Lines in space
|
||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||
|
Lines can be specified in a variety of ways. One way is described as follows. Select a point P0 on the line l, and a non-zero vector v parallel to the line. The line l is then the unique line passing through P0 and parallel to v. 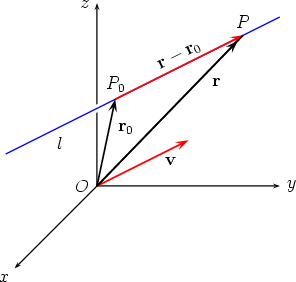
Now P lies on l if and only if 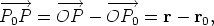 this condition is equivalent to r - r0 = tv for some scalar t. The equation 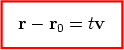
is called a parametric vector equation of the line l. (It is not unique, as a different point P0 on the line could have been chosen, changing r0, and v can be replaced by any other non-zero vector parallel to l.) Each value of the parameter t determines a unique point P, with position vector r = r0 + tv, on the line l. As t takes all possible values, P takes all possible positions on the line l.
|
|||||||||||||||||||||||||||||||||||||||||
| Feedback |
|
|||||||||||||||||||||||||||||||||||||||||
© 2002-09 The University of Sydney. Last updated: 09 November 2009
ABN: 15 211 513 464. CRICOS number: 00026A. Phone: +61 2 9351 2222.
Authorised by: Head, School of Mathematics and Statistics.
Contact the University | Disclaimer | Privacy | Accessibility
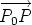 is parallel to
is parallel to