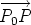|
||||||||||||||||||||||||||||||||||||
|
13. Planes in space
|
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
A plane can be described in many ways. The plane, for example, can be specified by three non-collinear points of the plane: there is a unique plane containing a given set of three non-collinear points in space. An alternative way to specify a plane is given as follows. Select a point P0 in the plane. There is a unique line through P0 perpendicular to the
plane. This line is called the normal to to the plane at P0. A vector n There is a unique plane which passes through P0 and has n as a normal vector. 
Now P lies in the plane through P0 perpendicular to n if and only if As 
This is a vector equation of the plane.
|
|||||||||||||||||||||||||||||||||||
| Feedback |
|
|||||||||||||||||||||||||||||||||||
© 2002-09 The University of Sydney. Last updated: 09 November 2009
ABN: 15 211 513 464. CRICOS number: 00026A. Phone: +61 2 9351 2222.
Authorised by: Head, School of Mathematics and Statistics.
Contact the University | Disclaimer | Privacy | Accessibility
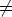
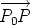 and
and