 |
||||||||||||||||||||||||||||||
|
14. Line Vectors
|
||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
|
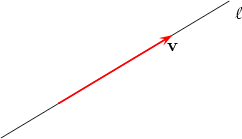
The theory of vectors is the appropriate mathematical language for dealing with forces. In order to specify the effect of a force on a rigid body we need to give the direction, the magnitude and the point of application. The first two properties, namely direction and magnitude, indicate that we are dealing with a vector quantity. The third property, namely the point of application, means that we need some additional information. In dealing with forces it turns out that it is only the line of application that matters and not the particular point on the line. This leads us to the next definition. A line vector is a pair (
|
|||||||||||||||||||||||||||||
| Feedback |
|
|||||||||||||||||||||||||||||
© 2002-09 The University of Sydney. Last updated: 09 November 2009
ABN: 15 211 513 464. CRICOS number: 00026A. Phone: +61 2 9351 2222.
Authorised by: Head, School of Mathematics and Statistics.
Contact the University | Disclaimer | Privacy | Accessibility
 ,
,