The University of Sydney - School of Mathematics and Statistics

Coordinate axes and Cartesian coordinates	Page 1 of 5

By three dimensional space we mean the space we live in. To fix a point P in three dimensional space requires a system of axes and three numbers. First select any point, call it the origin and mark it as O. All measurements will from now on originate from this point O. Next place three mutually perpendicular axes OX, OY , OZ through O. This axis system is drawn on a page like this: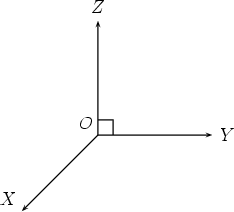

Note that although it may not look it, the angles XOY , XOZ, Y OZ are all right-angles!

To fix any given point P in three dimensional space, we refer it to the axis system. Let us first show the point P and the coordinate axes.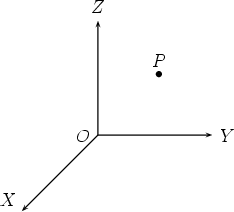

1. Drop a line from P perpendicular to the XOY plane (think of this plane as the floor), meeting the XOY plane at a point Q (the foot of the perpendicular).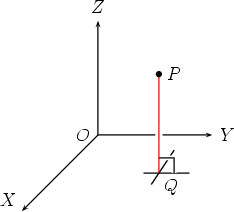

2. Now we are in the XOY plane with a point Q and an axis system in two dimensions.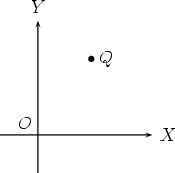

3. Drop a perpendicular from Q to OX and OY .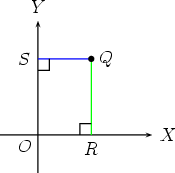

4. Transfer the two-dimensional picture from 3 into the three dimensional diagram from 1.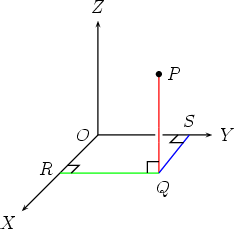

(Some of the right angles are marked: you should mark all the other right angles in the picture.)

5. Measure the lengths OR, OS, QP, and denote them by x, y, z respectively. We call the three numbers (x,y,z), in the order given, the Cartesian coordinates of the point P.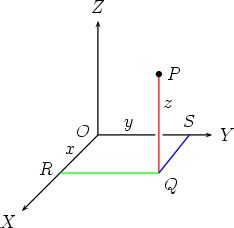

Notice that the order in which the numbers are written is important: (1, 2, 1) and (2, 1, 1) are the Cartesian coordinates of different points.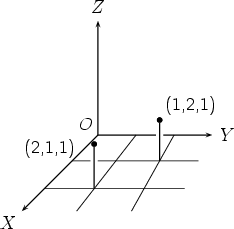

To make the diagrams uncluttered, only half of each axis has been drawn. However, if the axes are extended infinitely in both directions, it can be seen that this axis system creates eight octants in space, just as the two dimensional axis system creates four quadrants in the plane. Points in the eight different octants have Cartesian coordinates corresponding to all possible combinations of positive and negative values of x, y and z. The figures above illustrate points in the octant corresponding to positive values of x, y and z.