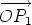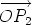|
||||||||||||||||||||||||||||||||||||||||||
|
7. Cartesian coordinates in three dimensions
|
||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||
|
Given two vectors in Cartesian form 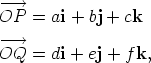
the sum 
It can be proved that this is the same as the following calculation: 
That is, the components of a sum are the sums of the components. Notice that the parallelogram OQRP is part of a two dimensional plane sitting within three dimensional space (in a tilted way like the slanting face of the roof of a house).
SubtractionThe rule for subtraction works in exactly the same way. Writing 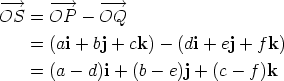
The subtraction is illustrated below. Recall that 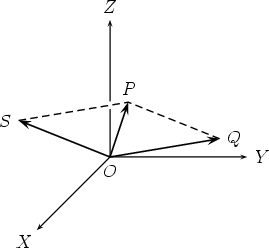
An example of the use of this rule is the calculation of the Cartesian form of the
position vector Then 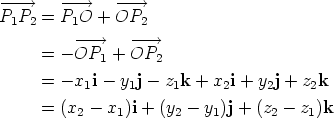
|
|||||||||||||||||||||||||||||||||||||||||
| Feedback |
|
|||||||||||||||||||||||||||||||||||||||||
© 2002-09 The University of Sydney. Last updated: 09 November 2009
ABN: 15 211 513 464. CRICOS number: 00026A. Phone: +61 2 9351 2222.
Authorised by: Head, School of Mathematics and Statistics.
Contact the University | Disclaimer | Privacy | Accessibility
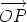
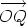
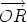 is obtained by completing the parallelogram.
is obtained by completing the parallelogram.  for the vector
for the vector
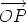
 , the rule above gives
, the rule above gives
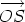

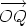
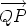 .
.
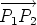 of a point
of a point