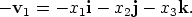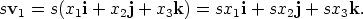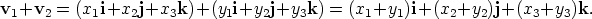|
||||||||||||||||||||||||||||||
|
8. Vector algebra
|
||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
|
We discuss properties of the two operations, addition of vectors and multiplication of a vector by a scalar, but now for vectors in Cartesian form. Suppose vectors v1 and v2 are written in Cartesian form, 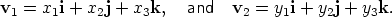
|
|||||||||||||||||||||||||||||
| Feedback |
|
|||||||||||||||||||||||||||||
© 2002-09 The University of Sydney. Last updated: 09 November 2009
ABN: 15 211 513 464. CRICOS number: 00026A. Phone: +61 2 9351 2222.
Authorised by: Head, School of Mathematics and Statistics.
Contact the University | Disclaimer | Privacy | Accessibility