A Celebration of Norman Dancer’s 60th Birthday
University of New England (Armidale), Australia, 16-21 July 2006
Marek Izydorek
Gdansk University of Technology (Poland)Generalized heteroclinic solutions for a class of the second order Hamiltonian systems
We shall be concerned with the existence of heteroclinic orbits for the second order Hamiltonian system
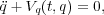 | (HS) |
where q  Rn and V
Rn and V  C1(R ×Rn,R), V ≤ 0. We will assume that V and a certain subset M ⊂ Rn satisfy the
following conditions:
C1(R ×Rn,R), V ≤ 0. We will assume that V and a certain subset M ⊂ Rn satisfy the
following conditions:
- #M ≥ 2 and
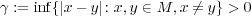 ,
,
- there exists 0 < ɛ0 ≤ G such that for every 0 < ɛ ≤ ɛ0 there is δ > 0 such that for all (t,x)
 R×Rn
if d(x,M) ≥ ɛ then -V (t,x) > δ,
R×Rn
if d(x,M) ≥ ɛ then -V (t,x) > δ,
- for every x
 Rn \ M,
Rn \ M, 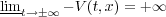 ,
,
- for every x
 M,
M, 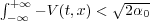 , where
, where
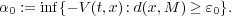
Our result states that each point of M is joined with a certain other element of M by a solution of (HS). Since
we should not expect that (HS) possesses a stationary solution the notion of a heteroclinic orbit is
used in a generalized sense. Namely, q: R → Rn is a generalized heteroclinic solution of (HS) if
there exist x,y  Rn, x≠y such that q joins x to y, (i.e. limt→-∞q(t) = x, limt→+∞q(t) = y).
Rn, x≠y such that q joins x to y, (i.e. limt→-∞q(t) = x, limt→+∞q(t) = y).