A Celebration of Norman Dancer’s 60th Birthday
University of New England (Armidale), Australia, 16-21 July 2006
Angela Pistoia
Universitá di Roma 1 (Italy)On the existence of sign changing solutions for the Bahri-Coron problem
Let Ω be a bounded smooth domain in RN, N ≥ 3 and p = N+2 N-2. We are interested in existence and multiplicity of sign changing solutions to the slightly subcritical problem
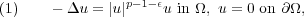
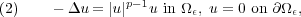
- T. Bartsch, A.M. Micheletti, A. Pistoia, On the existence and the profile of nodal solutions of elliptic equations involving critical growth, Calc. Var. Partial Differential Equations (to appear).
- M. Musso, A. Pistoia, Sign changing solutions to Bahri-Coron’s problem in pierced domains, (preprint).
- A. Pistoia, T. Weth, Sign changing bubble tower solutions in a slightly subcritical semilinear Dirichlet problem, Ann. Inst. H. Poincaré Anal. Non Linéaire (to appear).