Slawomir M. Rybicki

Global bifurcations of solutions of elliptic systems

The aim of my talk is to present Rabinowitz alternative for systems of elliptic differential equations of the form

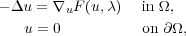
where

1. Ω ⊂ R^N is an open, bounded subset of R^N, with boundary of the class C^1-,
2. F C²(R^m × R,R),
3. dsF(x,λ) = 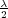⟨Ax,x⟩ + η(x,λ), where
   1. A is a symmetric (m × m)-matrix,
   2. ∇_xη(0,λ) = 0, for any λ R,
   3. ∇_x²η(0,λ) = 0, for any λ R,
4. there are C > 0 and 1 ≤ p < (N + 2)(N - 2)^-1 such that for any (x,λ) Rⁿ ×R the following inequality holds true |∇_xF(x,λ)|≤ C.