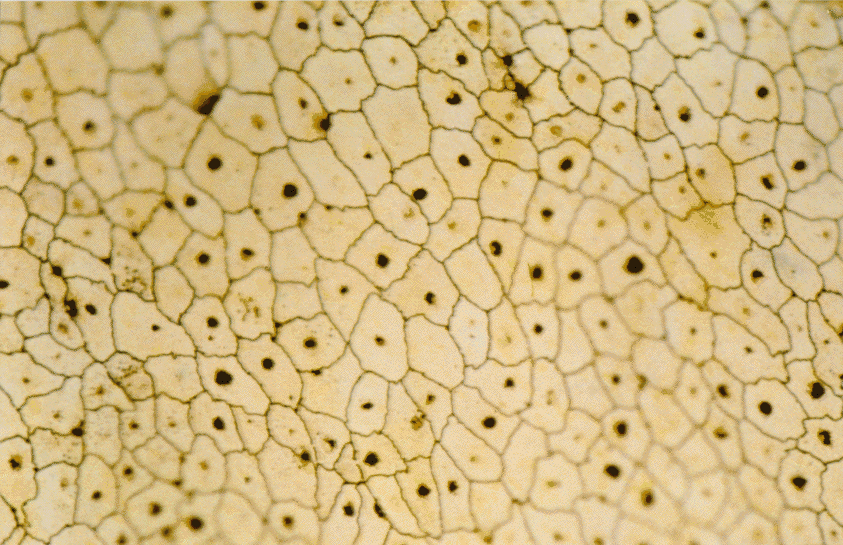
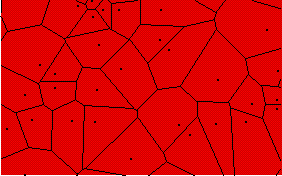
The Voronoi tessellation constructed from particles which form a Poisson process. Each polygon contains one particle and comprises the region of the plane closer to that particle than to any other.

There are no edge effects in this picture, as the figure was constructed initially on a much larger domain.

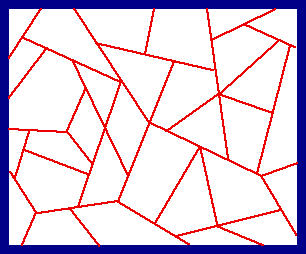Random tessellations can be quite general in character, with vertices of all orders and polygons of all sizes and shapes. A general theory of ergodic homogeneous tessellations is developed in #10 and #14.

Results include the first proofs (and correct statement) of topological linkage formulae

where, for the typical polygonal cell, assumed convex,

and, for the typical vertex, θ = the mean # of arms and φ = the proportion of vertices which have an angle of 180 degrees between two of its adjacent arms. Note: φ is the phi in the formula.

This is an example of the "falling-leaf" tessellation, studied in #58.

Congruent polygonal leaves fall randomly onto the plane covering leaves which have fallen earlier. Our interest is the random tessellation formed by the leaf edges when temporal equilibrium is reached.

Results are given in #58 for stochastic properties of the tessellation's polygons and vertices (even when shapes are more elaborate, with curved edges).

This is a small part of the pigment epithelium in the chick eye. Photo taken by Valerie Morris, who has kindly provided it for this page.

During development, these cells (which are in a 2-d sheet) grow and then divide, with a division plane roughly orthogonal to the plane of this picture. These planes are seen as lines in the picture. When first formed, the division "line" forms two T-junctions at either end (as can be seen for a recently divided cell in the top left corner of the photo.)

Later, the line contracts and pulls the T-junctions into a Y-form. Pressure differentials within cells create curvature in the lines.

This is another epithelium, in the stomach of humans. Photo provided by the Department of Anatomy at the University of Hong Kong.

Question: How to estimate the variance of the cellular areas, with due account for edge effects in the photo? Information from the cells truncated by the boundary cannot be ignored. Nor are the cells wholly enclosed in the field of view representive of all cells (if the field is not large).

This type of question is studied by statisticians working with spatial patterns.