Geometry & Groups

AMSI Summer School 2012 at the University of New South Wales

updates

8 February 2012: You can e-mail Assignment 4 to me by Friday, 10 February, at 24:00. Sydney based students can also drop it off at the exam at UNSW.
3 February 2012: Exercises up-dated. Information about the exam added.

synopsis

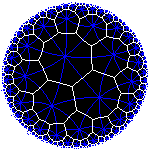
According to Felix Klein's influential Erlanger program of 1872, geometry is the study of properties of a space, which are invariant under a group of transformations. In Klein's framework, the familiar Euclidean geometry consist of n-dimensional Euclidean space and its group of isometries. In general, a geometry is a pair (X, G), where X is a (sufficiently nice) space and G is a (sufficiently nice) group acting on the space. Geometric properties are precisely those that are preserved by the group. A geometry in Klein's sense may not allow the concepts of distance or angle; an example of this is affine geometry.

The study of geometry in Klein's framework motivates key ideas in different areas of mathematics, such as group theory, algebraic topology, differential geometry and representation theory. The seminal work of Bill Thurston has provided even more links between seemingly disparate fields of mathematics.

The aim of this course is to give students an introduction to geometry in the sense of Klein and Thurston, and to provide them with working knowledge of a variety of concepts and tools that are applicable in different fields of mathematics, as well as to open avenues for further study. A great emphasis will be placed on the detailed study of key examples.

quick overview

Week 1: Model geometries in dimension two
Week 2: Notions from group theory and algebraic topology
Week 3: Hyperbolic geometry
Week 4: Geometric structures on manifolds

detailed overview (pdf)

textbook

Low-Dimensional Geometry: From Euclidean Surfaces to Hyperbolic Knots by Francis Bonahon
Student Mathematical Library, 49. IAS/Park City Mathematical Subseries.
American Mathematical Society, Providence, RI; Institute for Advanced Study (IAS), Princeton, 2009.
A list of errata for the book by Francis Bonahon.

materials

The following materials were handed out in lectures. Please ask me for a copy if you don't have them:

contact hours

Feel free to approach me during morning tea, or to look for me in room 4071 in the Red Centre.
You can also make an appointment for consultation by e-mail.

prerequisites

Essential: A course in Multivariable Calculus and a course in Linear Algebra.
Based on the background knowledge feedback, I will assume that you are comfortable with the material from:

After week 1, read through all of 2.1-2.15, and all of 3.1-3.7.

bed-time reading

These books are really enjoyable to read. They give nice introductions and contain excellent illustrations.

games

These geometry games by Jeffrey Weeks can help to gain some intuition about tilings, curvature and group actions:

You are especially encouraged to explore the hyperbolic games, and to go through the study questions, which are accessible through the games' help menu.

assessment (overview)

3 short assignments (total 30% of your final mark)
1 long assignment (total 20% of your final mark)
final exam (total 50% of your final mark)

assessment (short assignments)

The assignments will be given out in the last lecture of each week.

Assignment 1 (due Tuesday, 17 January, 9:00)
Assignment 2 (due Tuesday, 24 January, 9:00)
Assignment 3 (due Monday, 30 January, 9:00)

assessment (long assignment)

The format will be determined once I know the number of students taking the course for credit.

assessment (final exam)

The final exam is worth 50% of the final mark and covers material from the entire course.

Time and date: TBA
(10 min perusal; 120 min duration)

The exam may include the following:

1) explicit examples or computational questions
— e.g. 5.2, 5.9
2) short, rigorous proofs
— e.g. 2.2, 7.4
3) ask you to state theorems/definitions
— e.g. any theorem that has a name and any key definition; useful results such as the classification of isometries
4) applications of major theorems
— e.g. show that a given quotient semi-metric is a metric using the corollary of the "useful lemma" given in Lecture 5
5) questions that require insight
— e.g. 10.1, 10.2, 10.3
6) proofs or examples from the lectures or assignments

As to 6): If I ask you to prove something, it should be straight forward. For long or involved proofs that were covered in lectures, I don't expect you to know all the details, but rather to know the storyline, and the main points. For example, I expect you to know how and where the discontinuity of the action is used to show that the Dirichelet domain is locally finite (in the 2-d proof given in class). As another example, I expect you to know why Theorem 7.7 is true.

suggested exercises

I'm listing below some exercises from the book that were either given in lectures as explicit exercises, or include details that were left for you to check, plus some additional problems.
You should also keep track of other exercises that I set during lectures.

Bonahon, Chapter 1

1.1, 1.2, 1.3

Bonahon, Chapter 2

2.2, 2.4, 2.9, 2.10, 2.11, 2.12, 2.13, 2.16, 2.17

Bonahon, Chapter 3

3.1

Bonahon, Chapter 4

4.1, 4.4, 4.5

Bonahon, Chapter 5

5.2, 5.5, 5.9, 5.13, 5.16

Bonahon, Chapter 6

6.8, 6.10, 6.11, 6.12, 6.14, 6.15

Bonahon, Chapter 7

7.2, 7.4, 7.5, 7.6, 7.12, 7.13, 7.14

Bonahon, Chapter 9

9.1, 9.10, 9.11, 9.12

Bonahon, Chapter 10

10.1, 10.2, 10.3

Bonahon, Chapter 12

12.4, 12.7

references

A number of books are on reserve in the library.

feedback

Please let me know if you have any problems or comments on the subject; both with regard to the contents and how it is run.