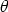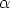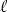|
||||||||||||||||||||||||||||||||||||
|
11. The vector product
|
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
Unless one (or both) of the vectors is zero, it is not obvious how to get the formula to compute the vector product from the geometric definition of the vector product. If you are interested in how to obtain it, here is a possible way. The procedure depends on looking at projections of the parallelograms spanned by the vectors u and v into the three coordinate planes. We proceed in three steps.
Step 1We first look at vectors in the xy-plane. The magnitude of u × v is 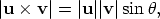
so u×v = ±(|u||v| sin 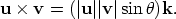
(We use that sin(- 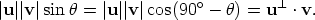 Two possible situations are shown below 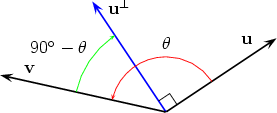
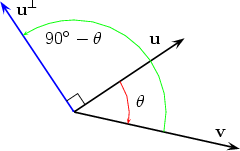
We therefore get u × v = (u Now assume that u = u1i + u2j and v = v1i + v2j. Then from the figure below
u 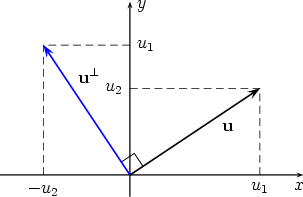
Using the formula for the scalar product we get 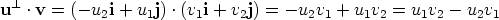
and therefore u × v = (u
Step 2Let now u and v be two non-zero and non-parallel vectors in space. Denote by P the parallelogram they span when placed tail-to-tail. By definition of the vector product the area of P is A = |u × v|. We now project P along the z-axis onto the xy-plane. That projection, P', is spanned by the projections u' and v' of u and v onto the xy-plane. It will be shown in Step 3 that the area, A', of P' is given by 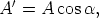
where Observe that Writing w = w1i + w2j + w3k it follows that 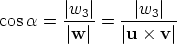 as you see from the figures below, representing a cross section along w and the z-axis. 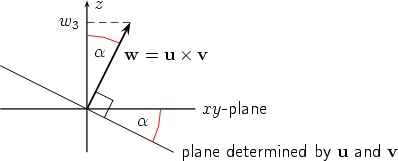
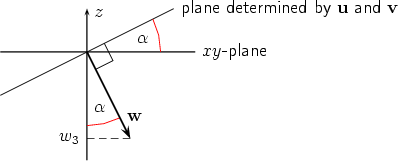
If w3 > 0 the triple u', v', k is right handed, otherwise it is left handed. Hence by the definition of the vector product u'× v' = w3k. If we note that u' = u1i + u2j and v' = v1i + v2j we conclude from Step 1 that w3 = u1v2 - u2v1. We get the other components w1 and w2 by the cyclic permutation i
Step 3We determine how the area of a parallelogram is changed when it is projected onto a
plane. Suppose that E1 and E2 are two planes intersecting at a line 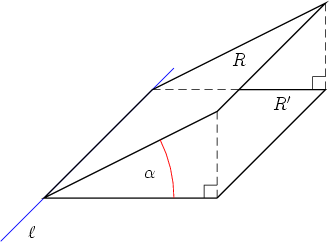
Now look at an arbitrary parallelogram P on E2 spanned by vectors u and v. We can
transform it into a rectangle of the same area such that one edge of that rectangle is
parallel to 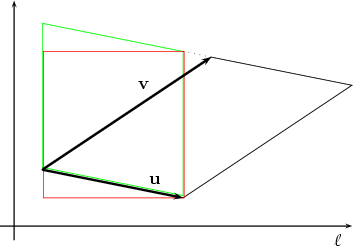
The projections of the black, green and red parallelograms into E1 have all the same area as the picture looks very similar in E1. Suppose the area of the original black parallelogram is A2 and that of its projection is A1. Then the area of the red rectangle is A2 and that of its projection is A1. From the previous considerations we know that 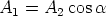
with
|
|||||||||||||||||||||||||||||||||||
| Feedback |
|
|||||||||||||||||||||||||||||||||||
© 2002-09 The University of Sydney. Last updated: 09 November 2009
ABN: 15 211 513 464. CRICOS number: 00026A. Phone: +61 2 9351 2222.
Authorised by: Head, School of Mathematics and Statistics.
Contact the University | Disclaimer | Privacy | Accessibility