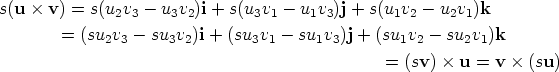The University of Sydney - School of Mathematics and Statistics

The algebraic rules of the vector product	Page 4 of 7

The vector product obeys the following algebraic rules

Warning

The expression (u × v) × w makes sense, but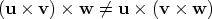

in general. As a counterexample look at (i × i) × j. We have (i × i) × j = 0 × j = 0 but i × (i × j) = i × k = -j.

This shows that writing u × v × w does not make sense as it is not clear which two vectors to multiply first!

The easiest way to prove the algebraic rules of the vector product is to make use of the Cartesian representation of the vector product. Hence assume that u = u₁i + u₂j + u₃k, v = v₁i + v₂j + v₃k and w = w₁i + w₂j + w₃k.

1. u×v = -(v×u) follows directly from the definition of the vector product;
2. For every scalar s
3. Using the Cartesian representations we get