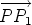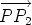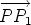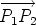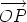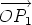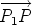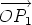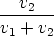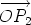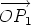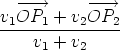|
Line vectors in two dimensions
| Page 4 of 4 |
If ( 1,v1) and ( 1,v1) and ( 2,v2) are line vectors in two dimensions, then often (but not always)
it is possible to combine them into a single equivalent line vector ( 2,v2) are line vectors in two dimensions, then often (but not always)
it is possible to combine them into a single equivalent line vector ( ,R), where
R = v1 + v2. ,R), where
R = v1 + v2.
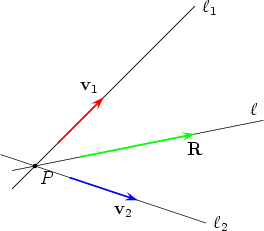
Suppose that the lines  1 and 1 and  2 have a point P in common. That is P is on both 2 have a point P in common. That is P is on both  1
and 1
and  2. This will always happen when 2. This will always happen when  1 and 1 and  2 are not parallel and it is also true
when 2 are not parallel and it is also true
when  1 and 1 and  2 are the same line. 2 are the same line.
Let R = v1 + v2 and let  be the line through P in the direction of R. In this case
the moments of ( be the line through P in the direction of R. In this case
the moments of ( 1,v1) and ( 1,v1) and ( 2,v2) about P are both 0 and so is the moment of
( 2,v2) about P are both 0 and so is the moment of
( ,R) about P. Therefore the single line vector ( ,R) about P. Therefore the single line vector ( ,R) is equivalent to the system
( ,R) is equivalent to the system
( 1,v1), ( 1,v1), ( 2,v2). 2,v2).
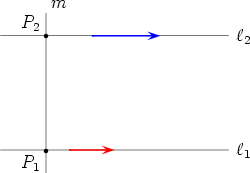
Now suppose that  1 and 1 and  2 are distinct parallel lines and that R = v1 + v2 is
not the zero vector. We can choose a point P1 on 2 are distinct parallel lines and that R = v1 + v2 is
not the zero vector. We can choose a point P1 on  1 and a point P2 on 1 and a point P2 on  2
such that the line m through P1 and P2 is perpendicular to both 2
such that the line m through P1 and P2 is perpendicular to both  1 and 1 and
 2. 2.
Let 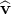 be a unit vector in the direction of v1. Then there are scalars v1 and v2 such
that v1 = v1 be a unit vector in the direction of v1. Then there are scalars v1 and v2 such
that v1 = v1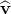 and v2 = v2 and v2 = v2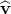 . Put w = . Put w =  and suppose that and suppose that 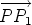 = aw. = aw.
Then 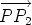 = = 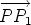 + + 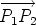 = (a + 1)w and so av1 + (a + 1)v2 = 0. From
this it follows that a = -v2/(v1 + v2) and therefore, for any point O we
have = (a + 1)w and so av1 + (a + 1)v2 = 0. From
this it follows that a = -v2/(v1 + v2) and therefore, for any point O we
have
Thus P divides the line segment P1P2 in the ration v2 : v1.
Couples
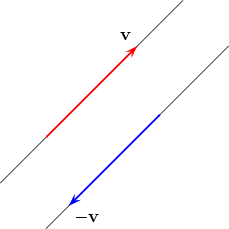
If the vectors v1 and v2 have equal magnitude but opposite direction, then
v1 + v2 = 0 and it is not possible to find a single line vector that is equivalent to the
pair ( 1,v1) and ( 1,v1) and ( 2,v2). In this case the system of two line vectors ( 2,v2). In this case the system of two line vectors ( 1,v1) and
( 1,v1) and
( 2,v2) is called a couple. When the forces applied to a rigid body form a couple, the
effect is pure twist without any translation. 2,v2) is called a couple. When the forces applied to a rigid body form a couple, the
effect is pure twist without any translation.
|


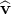 be a unit vector in the direction of
be a unit vector in the direction of 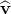 and
and 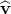 . Put
. Put  and suppose that
and suppose that