 |
||||||||||||||||||||||||||||||||||||
|
5. Division of a line segment
|
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
We look at a situation similar to the one on the
previous page, but allow m and n to have opposite sign. Again, R is the point such
that 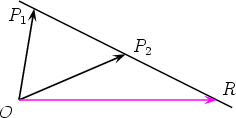
Since The point R then lies outside the line segment P1P2 (but still on the line joining P1 and P2). In these cases, R is said to divide the line segment P1P2 externally in the ratio m : n. The formula is, as in case of an internal division, 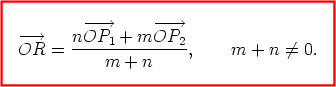
|
|||||||||||||||||||||||||||||||||||
| Feedback |
|
|||||||||||||||||||||||||||||||||||
© 2002-09 The University of Sydney. Last updated: 09 November 2009
ABN: 15 211 513 464. CRICOS number: 00026A. Phone: +61 2 9351 2222.
Authorised by: Head, School of Mathematics and Statistics.
Contact the University | Disclaimer | Privacy | Accessibility
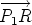
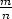
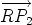 , and we want to find the position vector of
, and we want to find the position vector of 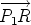 is a negative multiple of
is a negative multiple of 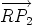 , the vectors
, the vectors 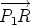 and
and 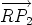 have opposite
direction.
have opposite
direction.