The University of Sydney - School of Mathematics and Statistics

Coordinate axes and Cartesian coordinates	Page 1 of 4

By two dimensional space we mean a plane surface extending infinitely in all directions. A table top, for example, is a subset of two dimensional space. To fix a point Q in two dimensional space requires two numbers. First select any point, call it the origin and mark it as O. All measurements will from now on originate from this point O. Next place two mutually perpendicular axes OX, OY through O. Within this reference frame we look for the given point Q, shown in the diagram below.

Drop perpendiculars from Q to OX and OY .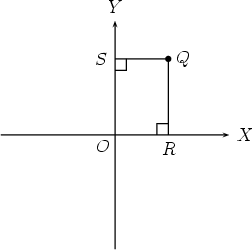

Every point on the OX axis corresponds to a real number: by convention, positive numbers to the east of O and negative numbers to the west of O. Similarly, every point on the OY axis also corresponds to a real number: positive numbers to the north of O and negative numbers to the south of O. Thus in the diagram above, both R and S correspond to positive numbers, say x and y respectively. We call the pair of numbers (x,y) the Cartesian coordinates of the point Q. Notice that the order in which the numbers are written is important: (1, 2) and (2, 1) are the Cartesian coordinates of different points.

All points in the first quadrant have Cartesian coordinates (x,y) in which x and y are both positive. Points in the second quadrant have coordinates (x,y) in which x is negative and y is positive, points in the third quadrant have coordinates (x,y) in which both x and y are negative, and points in the fourth quadrant have coordinates (x,y) in which x is positive and y is negative.