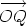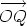|
||||||||||||||||||||||||||||||
|
6. Cartesian and polar coordinates in two dimensions
|
||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
|
After defining a coordinate system XOY we
introduce two basic vectors, namely a vector of length one in the direction of the
positive OX axis, and a vector of length one in the direction of the positive OY axis.
By convention, these unit vectors are called called i and j, respectively. Let r be any
vector parallel to the XOY plane. Then by translating r so that its tail is at the point
O, there is a unique point Q in the XOY plane such that r = 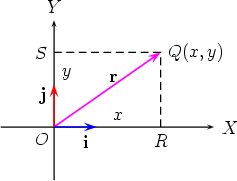
The vector 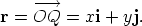 This formula, which expresses r in terms of i, j, x and y, is called the Cartesian representation of the vector r in two dimensions. We say x is the component of r along the OX axis and y is the component of r along the OY axis. The formula r = 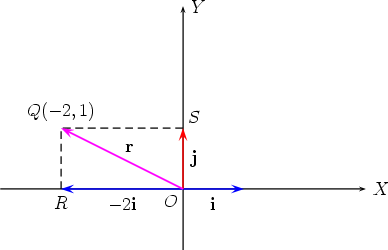
|
|||||||||||||||||||||||||||||
| Feedback |
|
|||||||||||||||||||||||||||||
© 2002-09 The University of Sydney. Last updated: 09 November 2009
ABN: 15 211 513 464. CRICOS number: 00026A. Phone: +61 2 9351 2222.
Authorised by: Head, School of Mathematics and Statistics.
Contact the University | Disclaimer | Privacy | Accessibility
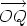 . If
. If 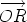 is equal to
is equal to 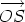 is equal to
is equal to 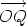 is the sum of
is the sum of 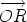 and
and 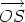 and therefore
and therefore