Talks in 2020
- Kyeongsu Choi, Ancient mean curvature flow and singularity analysis, Monday, 28 September 2020.
- Tadahisa Funaki, Motion by mean curvature and coupled KPZ from particle systems, Monday, 25 May 2020.
-
Benjamin Gess,
Large deviations for conervative, stochastic PDE and non-equilibrium fluctuations
Monday, 21 December 2020.
-
Changfeng Gui,
New Sharp Inequalities in Analysis and Geometry,
Monday, 1 June 2020.
- Hitoshi Ishii, The vanishing discount problem for systems of Hamilton-Jacobi equations , Monday, 18 May 2020.
- Soonsik Kwon, On pseudoconformal blow-up solutions to the self-dual Chern-Simons-Schrödinger equation , Monday, 8 June 2020.
- Yi Lai, A family of 3D steady gradient solitons that are flying wings , Monday, 30 November 2020.
-
Mathew Langford,
The atomic structure of ancient grain boundaries
,
Monday, 26 October 2020.
-
Martin Li,
Mean curvature flow with free boundary
,
Monday, 22 June 2020.
-
Yanyan Li,
Gradient estimates for the insulated conductivity problem
,
Monday, 2 November 2020.
-
Felix Otto,
A variational approach to the regularity theory for optimal transportation
,
Monday, 9 November 2020.
- Francesco Maggi, Symmetry results for Plateau's surfaces , Tuesday, 17 November 2020.
- Akihiko Miyachi, Some recent results on multilinear pseudo-differential operators with exotic symbols , Monday, 15 June 2020.
-
Connor Mooney,
The Bernstein problem for elliptic functionals
,
Monday, 29 June 2020.
- Shohei Nakamura,
Maximal estimates for the Schrödinger equation with
orthonormal initial data
,
Monday, 7 September 2020.
-
Michael Röckner,
The evolution to equilibrium of solutions to nonlinear Fokker-Planck
equations
,
Monday, 14 September 2020.
-
Daniel Spector,
Optimal Lorentz Estimates for Div-Curl Systems
,
Monday, 19 October 2020.
-
Keisuke Takasao,
Phase field method for volume preserving mean curvature flow
,
Monday, 7 December 2020.
-
Feng-Yu Wang,
Exponential Convergence in Entropy of McKean-Vlasov SDEs
,
Monday, 14 December 2020.
-
Zhenfu Wang,
Quantitative Methods for the Mean Field Limit Problem
,
Monday, 12 October 2020.
-
Glen Wheeler,
Current progress in higher-order curvature flow
,
Tuesday, 6 October 2020.
-
Chao Xia,
Recent progress on a sharp lower bound for Steklov eigenvalue
,
Monday, 11 May 2020.
-
Shiwu Yang,
Asymptotic decay for semilinear wave equation
,
Monday, 6 July 2020.
-
Pin Yu,
On the rigidity from infinity for nonlinear
Alfvén waves
,
Monday, 31 August 2020.

Professor @ Max Planck Institute for Mathematics in the Sciences, Leipzip, Germany
Professor Gess received his PhD 2011 @ the University of Bielefeld, Germany under
the supervision of Michael Röckner. After Postdoc positions @ the University
of Bielefeld, TU Berlin, Humboldt University Berlin, and the University of Chicago from 2012-2015,
he was a pointed as Academic Fellow @ the University of Bielefeld in 2015. Since 2016, Gess
became reseach group leader at the Max-Planck Institute for Mathematics in the Sciences,
Leipiz and got promoted to Professor (W2 in 2016 and W3 in 2019) @ the University of Bielefeld.
|
Large deviations for conservative, stochastic PDE and non-equilibrium fluctuations
Macroscopic fluctuation theory provides a general framework for far from equilibrium thermodynamics, based on a fundamental formula for large fluctuations around (local) equilibria. This fundamental postulate can be informally justified from the framework of fluctuating hydrodynamics, linking far from equilibrium behavior to zero-noise large deviations in conservative, stochastic PDE. In this talk, we will give rigorous justification to this relation in the special case of the zero range process. More precisely, we show that the rate function describing its large fluctuations is identical to the rate function appearing in zero noise large deviations to conservative stochastic PDE, by means of proving the Gamma-convergence of rate functions to approximating stochastic PDEs. The proof of Gamma-convergence is based on the well-posedness of the skeleton equation -- a degenerate parabolic-hyperbolic PDE with irregular coefficients, the proof of which extends DiPerna-Lions' renormalization techniques to nonlinear PDEs. See the video of the talk
on our YouTube Channel.
|

Cheung Kong Chair Professor @ Beijing Normal University, China
Professor Wang received his PhD in 1993 @ the Beijing Normal University in China, where he also accepted the offer of employment to a tenure track position afterwards. Wang was promoted Professor @ the Beijing Normal University in 1995, where he also has the prestigious title of Changjiang Chair Professor since 2000. Since 2007, Professor Wang parallel to his appointed at BNU also Research Professor @ Swansea University in the UK and since 2016, Professor @ the Tiajin University.
|
Exponential Convergence in Entropy of McKean-Vlasov SDEs
By using log-Harnack and Talagrand inequalities, the exponential convergence in entropy is proved for non-degenerate or degenerate Mckean-Vlasov SDEs. As applications, this type exponential convergence is confirmed for non- degenerate/degenerate granular media type equations generalizing existing studies on the exponential convergence in a mean field entropy studied by J. A. Carrillo, R. J. McCann, C. Villani (2003) and A. Guillin, W. Liu, L. Wu, C. Zhang (2019). See the video of the talk
on our YouTube Channel.
|
|
Associate Professor @ Kyoto University, Japan
Still to come
|
Exponential Convergence in Entropy of McKean-Vlasov SDEs
In 1993, Ilmanen proved a global existence of the weak solution to the mean curvature flow in the sense of the Brakke flow by using the phase field method. On the other hand, if we try to apply Ilmanen's proof to the volume preserving mean curvature flow, difficulties arise in the $L^2$-estimates of the non-local term. In this talk, we show a global existence of the weak solution in the sense of $L^2$-flow, in the $2$ or $3$-dimensional torus. We consider the Allen-Cahn equa+on with non-local term studied by Golovaty, and show the $L^2$-estimates of the non-local term and the monotonicity formula. As a recent result, we also prove a global existence of the weak solution to the mean curvature flow with forcing term in the suitable Sobolev space, by developing the method. See the video of the talk
on our YouTube Channel.
|
|
PhD student @ University of California at Berkeley, United States.
Yi Lai is currently a Ph.D. student at UC Berkeley under the supervision of Professor Richard Bamler. She got her Bachelor's degree from Peking University in 2016. Her research interests are in geometric analysis and particularly in Ricci flow.
|
A family of 3D steady gradient solitons that are flying wings
We found a family of \(\mathbb{Z}_2\times O(2)\)-symmetric 3D steady gradient Ricci solitons. We show that these solitons are all flying wings. This confirms a conjecture by Hamilton. See the video of the talk
on our YouTube Channel.
|

Professor @ University of Texas at Austin, United States.
Professor Maggi obtained his PhD in 2004 @
University of Firenze, Italy, under the supervision of Paolo
Marcellini. He was posdoctoral associate @ the Max Planck Institute
Leipzig, Germany, in 2004, associate professor @ the University
of Duisburg-Essen, Germany, in 2005, @ University of Firenze
from 2005-2011, @ University of Texas at Austin from 2012-2015,
and became full professor @ University of Texas at Austin in
2016. In addition, Professor Maggi was
research scientist at ICTP Trieste in Italy from 2016-2017 and was
a member of the Institute of Advanced Study, Princton, in 2019.
|
Symmetry results for Plateau's surfaces
By employing the method of moving planes in a novel way, we extend some classical symmetry and rigidity results for smooth minimal surfaces to surfaces that have singularities of the sort typically observed in soap films. This talk is based on joint work with Jacob Bernstein at Johns Hopkins University, appeared in preprint form on arXiv 2003.01784. See the video of the talk
on our YouTube Channel.
|

Director at the Max Planck Institute for Mathematics in the
Sciences, Leipzig and Honorary Professor for
Analysis and Mathematical Modelling, University of Leipzig.
Professor Otto obtained his PhD @ the University of Bonn,
Germany, in 1993 under the supervision of Stephan Luckhaus. From
1995-1996, Otto was a Visiting Scholar @ Courant Institute,
New York, in 1996 a Postdoctoral Associate @ Carnegie Mellon
University, Pittsburgh, and from 1996-1997 a postdoctoral
associate @ Courant Institute. In 1997, Otto obtained his
first tenure track position as Assistant Professor @ the
University of California at Santa Barbara, where he got promoted
as Full Professor in 1998. From 1999-2010, Otto held a
Professorship @ the University of Bonn, and since 2010,
Professor Otto is Director of the Max Planck Institute for
Mathematics in the Sciences in Leipzig, Germany.
|
A variational approach to the regularity theory for optimal transportation
The optimal transportation of one measure into another, leading to the notion of their Wasserstein distance, is a problem in the calculus of variations with a wide range of applications. The regularity theory for the optimal map is subtle and was pioneered by Caffarelli. This approach relies on the fact that the Euler-Lagrange equation of this variational problem is given by the Monge-Ampère equation. The latter is a prime example of a fully nonlinear (degenerate) elliptic equation, amenable to comparison principle arguments. We present a purely variational approach to the regularity theory for optimal transportation, introduced with M. Goldman. Following De Giorgi's philosophy for the regularity theory of minimal surfaces, it is based on the approximation of the displacement by a harmonic gradient through the construction of a variational competitor. This leads to a one-step improvement lemma, and feeds into a Campanato iteration on the \(C^{1,\alpha}\)-level for the optimal map, capitalizing on affine invariance. On the one hand, this allows to reprove the \(\varepsilon\)-regularity result (Figalli-Kim, De Philippis-Figalli) bypassing Caffarelli's celebrated theory. This also extends to boundary regularity (Chen-Figalli), which is joint work with T. Miura, and to general cost functions, which is joint work with M. Prodhomme and T. Ried. On the other hand, due to its robustness, it can be used as a large-scale regularity theory for the problem of matching the Lebesgue measure to the Poisson measure in the thermodynamic limit. This is joint work with M. Goldman and M. Huesmann. See the video of the talk
on our YouTube Channel.
|

Distinguished Professor @ Rutgers University, United States
Professor Li received his PhD in 1988 @ Courant Institute of
Mathematical Sciences, New York University. From 1988-1990, Li
was first employed as an instuctor @ Princton University, then
he obtained a tenure track position as Assistant Professor @
Rutgers University. In 1993, Li was promoted to Associate
Professor @ Rutgers and only four years later he got promoted to
Professor. Since 2000, Li is Distinguished Professor @ Rutgers
where he leads since 2010 the Center for Nonlinear Analysis.
|
Gradient estimates for the insulated conductivity problem
In this talk, we discuss the insulated conductivity problem with multiple inclusions embedded in a bounded domain in n-dimensional Euclidean space. The gradient of a solution may blow up as two inclusions approach each other. The optimal blow up rate was known in dimension \(n=2\). It was not known whether the established upper bound of the blow up rates in higher dimensions were optimal. We answer this question by improving the previously known upper bound of the blow up rates in dimension \(n>2\). This is a joint work with Zhuolun Yang. See the video of the talk
on our YouTube Channel.
|

Assistant Professor (Tenure Track) @ the University of
Tennessee Knoxville & ARC DECRA Fellow @ University of Newcastle, Australia.
Professor Langford obtained his PhD @ the Australian National
University (ANU) in Canberra, Australia, in 2015 under the
supervision of Ben Andrews and James McCoy. He was an Alexander
von Humboldt Fellow @ the Freie Universität Berlin from
2015-2017. Since August 2017, Langford is Associate Professor
(tenure track) @ the University of Tennessee Knoxville. Since
2020, Langford is on leave from UTK to carry out an ARC DECRA
Fellowship @ the University of Newcastle. Recently appeared
Professor Langford's new book on ''Extrinsic Geometric Flows''
(coauthored with Ben Andrews, Bennett Chow and Christine
Guenther)!
|
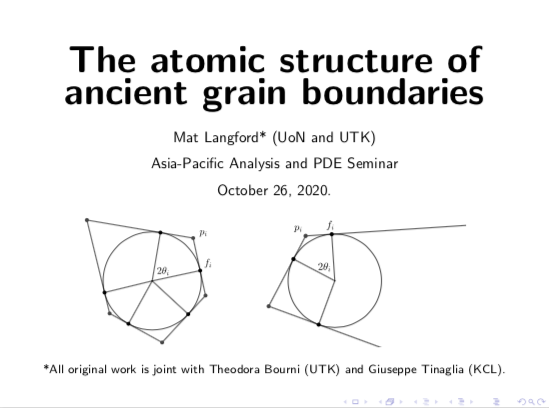
The atomic structure of ancient grain boundaries
I will present a series of far-reaching new existence and structure results for convex ancient solutions to mean curvature flow. An interesting picture (conjectured by Huisken and Sinestrari) emerges: convex ancient and translating solutions in slab regions decompose into certain canonical configurations of Grim Reapers, subject to certain necessary constraints. In particular, we construct new families of solutions with discrete symmetries as well as families of solutions which possess only a single reflection symmetry. These include many eternal solutions which do not evolve by translation (resolving a conjecture of White in the negative). Prior to these results, the only known examples were the rotationally symmetric ancient pancake and the rotationally symmetric flying wing translators. Several interesting questions remain open, however. This is joint work with Theodora Bourni and Giuseppe Tinaglia.
See the video of the talk
on our YouTube Channel.
|

Associate Professor @ Okinawa Institute of
Science and Technology Graduate University (OIST), Japan.
Professor Spector obtained his PhD in 2011 @ the Carnegie Mellon
University, United States under the supervision of Giovanni
Leoni. After his PhD, Spector was appointed as Distinguished
Assistant Professor @ the Zhejiang University, Hangzhou, China. From 2012
until 2014, he was a Postdoctoral Scholar @ the Technion
University in Haifa, Israel. From 2014 until 2019, Professor Spector
was appointed as Assistant Professor @ National Chiao Tung
University, Hsinchu, Taiwan, where was promoted to Associate
Professor in 2017. Since 2019, Spector is appointed as Associate
Professor @ OIST.
There are no slides to the talk! |
Optimal Lorentz Estimates for Div-Curl Systems
In a 2004 CR note and a 2007 JEMS paper, Jean Bourgain and Haim Brezis established the validity of some surprising estimates for elliptic systems in the \(L^1\) regime. It was an open problem in their 2007 paper whether one has an optimal Lorentz scale estimate for the Div-Curl system they consider. In this talk I will discuss the resolution of this problem, which has recently been obtained in collaboration with Felipe Hernandez. See the video of the talk
on our YouTube Channel.
|

Assistant Professor @ Beijing International Center for
Mathematical Research of the University of Peking, China.
Professor Wang obtained his PhD @ the University of Maryland in
2017. His PhD supervisor was Pierre-Emmanuel Jabin. He was a
Hans Rademacher Instructor of Mathematics @ the University of
Pennsylvania until September 2020. Since October 2020, Wang is
appointed to a tenur track Assistant professor
@ the Beijing International Center for
Mathematical Research of the University of Peking, China.
|
Quantitative Methods for the Mean Field Limit Problem
We study the mean field limit of large systems of interacting particles. Classical mean field limit results require that the interaction kernels be essentially Lipschitz. To handle more singular interaction kernels is a longstanding and challenging question but which now has some successes. Joint with P.-E. Jabin, we use the relative entropy between the joint law of all particles and the tensorized law at the limit to quantify the convergence from the particle systems towards the macroscopic PDEs. This method requires to prove large deviations estimates for non-continuous potentials modified by the limiting law. But it leads to explicit convergence rates for all marginals. This in particular can be applied to the Biot-Savart law for 2D Navier-Stokes. To treat more general and singular kernels, joint with D. Bresch and P.-E. Jabin, we introduce the modulated free energy, combination of the relative entropy that we had previously developed and of the modulated energy introduced by S. Serfaty. This modulated free energy may be understood as introducing appropriate weights in the relative entropy to cancel the most singular terms involving the divergence of the kernels. Our modulated free energy allows to treat gradient flows with singular potentials which combine large smooth part, small attractive singular part and large repulsive singular part. As an example, a full rigorous derivation (with quantitative estimates) of some chemotaxis models, such as the Patlak-Keller-Segel system in the subcritical regimes, is obtained. See the video of the talk
on our YouTube Channel.
|

Senior Lecturer @ University of Wollongong, Australia.
Professor Wheeler obtained his
PhD in 2010 @ the University of
Wollongong, Australia under the supervision of James McCoy and
Graham Williams.
|
Current progress in higher-order curvature flow
In this talk, we survey recent developments in higher-order curvature flow, with a focus on the most prominent fourth-order curvature flow: Willmore flow, surface diffusion flow, and Chen’s flow. We discuss these new developments in the context of big early successes, with a perspective to the current important open problems. See the video of the talk
on our YouTube Channel.
|

Professor @ Korea Institute for Advanced Study,
Korea.
Professor Choi received his PhD in
Mathematics in 2017 @ Columbia
University under the supervision of Professor
Panagiota Daskalopoulos. He was a C.L.E. Moore
Instructor @ MIT from 2017 – 2020. Since May 2020,
Choi is professor @ the Korea Institute for Advanced Study,
Korea.
|
Ancient mean curvature flow and singularity analysis
The mean curvature flow is a parabolic PDE for hypersurfaces. As like semi-linear heat equations, it develops singularities where we can find ancient solutions by blowing-up. Therefore, we can observe what happens at a singularity if we classify all ancient solutions from the singularity and figure out their nice properties. For example, we can show the well-posedness around stable singularities by proving that all ancient flows from them always have positive speed. Also, we can find a way to avoid unstable singularities by studying one-sided ancient flows. In this talk, we discuss some applications of ancient mean curvature flows. Also, we talk about how Angenent-Daskalopoulos-Sesum applied singularity analysis of semi-linear heat equations for classification of ancient flows. This is based on several joint works with Brendle, Chodosh-Mantoulidis-Schulze, and Haslhofer-Hershkovits-White. See the video of the talk
on our YouTube Channel.
|

Professor @ Bielefeld University, Germany and @ Academy of
Mathematics and Systems Science, CAS, China.
Professor Röckner obtained his PhD in 1984 @ Bielefeld
University, Germany under the supervision of Sergio Albeverio and
Christopher John Preston.
|
The evolution to equilibrium of solutions to nonlinear Fokker-Planck
equations
The talk is about the so-called \(H\)-Theorem for a class of nonlinear Fokker-Planck equations which are of porous media type on the whole Euclidean space perturbed by a transport term. We first construct a solution in the sense of mild solutions on \(L^1\) through a nonlinear semigroup of contractions. Then we study the asymptotic behavior of the solutions when time tends to infinity. For a large class \(M\) of initial conditions we show their relative compactness with respect to local \(L^1\)-convergence, while all limit points belong to \(L^1\). Under an additional assumption, we obtain that we in fact have convergence in \(L^1\), if the initial condition is a probability density. The limit is then identified as the unique stationary solution in \(M\) to the nonlinear Fokker-Planck equation. This solution is thus an invariant measure of the solution to the corresponding distribution dependent SDE whose time marginals converge to it in \(L^1\). It turns out that under our conditions the underlying nonlinear Kolmogorov operator is a (both in the second and first order part) nonlinear analog of the generator of a distorted Brownian motion. The solution of the above mentioned distribution dependent SDE can thus be interpreted as a nonlinear distorted Brownian motion. Our main technique for the proofs is to construct a suitable Lyapunov function acting nonlinearly on the path in \(L^1\), which is given by the nonlinear contraction semigroup applied to the initial condition, and then adapt a classical technique of Pazy to our situation. This Lyapunov function is given by a generalized entropy function (which in the linear case specializes to the usual Boltzmann-Gibbs entropy) plus a mean energy part. This is based on joint work with Viorel Barbu (Romanian Academy, Iasi). See the video of the talk
on our YouTube Channel.
|

Professor @ the Yau Mathematical Sciences Center, China.
Professor Yu obtained his PhD in 2010 @Princeton
University under the direction of Sergiu Klainerman and Igor
Rodnianski. He got the bachelor degree from the Peking
University in China and master degree from Ecole Polytechnique in France.
|
On the rigidity from infinity for nonlinear Alfvén waves
The Alfvén waves are fundamental wave phenomena in magnetized plasmas and the dynamics of Alfvén waves are governed by a system of nonlinear partial differential equations called the MHD system. In the talk, we will focus on the rigidity aspects of the scattering problem for the MHD equations: We prove that the Alfven waves must vanish if their scattering fields vanish at infinities. The proof is based on a careful study of the null structure and a family of weighted energy estimates. This is based on the joint work with Mengni Li. |

Assistant
Professor @ the Beijing International Center for Mathematical Research
Professor Yang obtained his PhD @Princeton
University in 2013. He was a senior research associate @ the
University of Cambridge from 2013-2016. Since 2016, he is an
Assistant Professor @ the Beijing International Center
for Mathematical research.
|
Asymptotic decay for semilinear wave equation
In this talk, I will report recent progress on global behaviors for solutions of energy subcritical defocusing semilinear wave equations with pure power nonlinearity. We prove that in space dimension 1 and 2, the solution decays in time with an inverse polynomial rate, hence giving an affirmative answer to a conjecture raised by Lindblad and Tao. In higher dimension, we obtain improved scattering results for the solutions. The proof is based on vector field method with new multipliers. These works are jointed with Dongyi Wei. See the video of the talk
on our YouTube Channel.
|

Assistant
Professor @ University of California, Irvine.
Professor Mooney received his Ph.D. @ Columbia University in 2015. He
was an NSF Postdoctoral Research Fellow @ UT Austin from 2015-16, and a
Postdoctoral Researcher @ ETH Zurich from 2016-18. Since 2018, he has
been an Assistant Professor @ University of California, Irvine.
|
The Bernstein problem for elliptic functionals
The Bernstein problem asks whether entire minimal graphs in $\mathbb{R}^{n+1}$ are necessarily hyperplanes. This problem was completely solved by the late 1960s in combined works of Bernstein, Fleming, De Giorgi, Almgren, Simons, and Bombieri-De Giorgi-Giusti. We will discuss the analogue of this problem for more general elliptic functionals, and some recent progress in the case $n = 6$. See the video of the talk
on our YouTube Channel.
|

Assistant Professor @The Chinese University of Hong Kong
Professor Li received his Ph.D. @Standford (United
States). His thesis advisor was Professor Richard Schoen. He was
a Postdoctoral Fellow @University of British Columbia,
Vancouver (Canada) from 2011 until 2013, and @Massachusetts
Institute of Technoogy from 2013 until 2014. Since 2014, he is
Assistant Professor @The Chinese University of Hong
Kong.
|
AbstractMean curvature flow (MCF) is the negative gradient flow for the area functional in Euclidean spaces, or more generally in Riemannian manifolds. Over the past few decades, there have been substantial progress towards our knowledge on the analytic and geometric properties of MCF. For compact surfaces without boundary, we have a fairly good understanding of the convergence and singularity formation under the flow. The corresponding boundary value problems, however, are relatively less studied. In this talk, we will discuss some recent results on MCF of surfaces with boundary. In the presence of boundary, suitable boundary conditions have to be imposed to ensure the evolution equations are well-posed. Two such boundary conditions are the Dirichlet (fixed or prescribed) and Neumann (free boundary or prescribed contact angle) boundary conditions. We will mention some new phenomena in contrast with the classical MCF without boundary. Using a new perturbation technique, we establish new convexity and pinching estimates for MCF with free boundary lying on an arbitrary convex barrier with bounded geometry. These imply the smooth convergence to shrinking hemispheres along the flow, provided that the surface is initially convex enough. This can be compared to Huisken’s celebrated convergence results for MCF in Riemannian manifolds. This is joint work with Sven Hirsch. (These works are partially supported by RGC grants from the Hong Kong Government.) See the video of the talk
on our YouTube Channel.
|
|
Professor @ the Tokyo Woman's Christian University, Japan.
Professor Miyachi received his Ph.D. @ the
University of Tokyo, Japan. He was Associate Professor @
Hitotsubashi University in Tokyo from 1983 until 1995. Since then he
was appointed to Professor @ the Tokyo Woman's Christian University.
|
AbstractThe theory of linear pseudo-differential operators is now well-known and, in particular, the mapping properties of linear pseudo-differential operators of Hörmander's class $S^m_{\rho, \delta}$ is well understood. Multilinear pseudo-differential operators were introduced by Coifman and Meyer before 1980 but detailed study of their mapping properties were developed after 2000. Some interesting facts peculiar to the multilinear case have been found. In this lecture, I survey some features of multilinear pseudo-differential operators and introduce some recent results concerning the multilinear version of Hörmander's class. This talk is based on joint works with Naohito Tomita (Osaka University) and Tomoya Kato (Gunma University). See the video of the talk
on our YouTube Channel.
|

Associate Professor @ Korea Advanced Institute of
Science and Technology, Daejeon, Korea
Professor Kwon received his Ph.D. at UCLA in
2008. Then he worked at Princeton University as an
instructor in 2008-2010. Since 2010, he is appointed as
Associate Professor at the Korea Advanced Institute of
Science and Technology, Daejeon, Korea.
|
AbstractIn this talk, I present a blow up construction - jointly with Kihyun Kim - on the self-dual Chern-Simons-Schrödinger equation (CSS), also known as a gauged nonlinear Schrödinger equation (NLS). CSS is $L^{2}$-critical, admits solitons, and has the psuedoconformal symmetry. These features are similar to the $L^{2}$-critical NLS. In this work, we consider pseudoconformal blow-up solutions under $m$-equivariance, $m\geq1$. Our result is threefold. Firstly, we construct a pseudoconformal blow-up solution $u$ with given asymptotic profile $z^{\ast}$: \[ \Big[u(t,r)-\frac{1}{|t|}Q\Big(\frac{r}{|t|}\Big)e^{-i\frac{r^{2}}{4|t|}}\Big] e^{im\theta}\to z^{\ast}\qquad\text{in }H^{1} \] as $t\to0^{-}$, where $Q(r)e^{im\theta}$ is a static solution. Secondly, we show that such blow-up solutions are unique in a suitable class. Lastly, yet most importantly, we exhibit an instability mechanism of $u$. We construct a continuous family of solutions $u^{(\eta)}$, $0\leq\eta\ll1$, such that $u^{(0)}=u$ and for $\eta>0$, $u^{(\eta)}$ is a global scattering solution. Moreover, we exhibit a rotational instability as $\eta\to0^{+}$: $u^{(\eta)}$ takes an abrupt spatial rotation by the angle \[ \Big(\frac{m+1}{m}\Big)\pi \] on the time interval $|t|\lesssim\eta$. We are inspired by works in the $L^{2}$-critical NLS. In the seminal work of Bourgain and Wang (1997), they constructed such pseudoconformal blow-up solutions. Merle, Raphaël, and Szeftel (2013) showed an instability of Bourgain-Wang solutions. Although CSS shares many features with NLS, there are essential differences and obstacles over NLS. Firstly, the soliton profile to CSS shows a slow polynomial decay $r^{-(m+2)}$. This causes many technical issues for small $m$. Secondly, due to the nonlocal nonlinearities, there are strong long-range interactions even between functions in far different scales. This leads to a nontrivial correction of our blow-up ansatz. Lastly, the instability mechanism of CSS is completely different from that of NLS. Here, the phase rotation is the main source of the instability. On the other hand, the self-dual structure of CSS is our sponsor to overcome these obstacles. We exploited the self-duality in many places such as the linearization, spectral properties, and construction of modified profiles. In the talks, I will present background of the problem, main theorems, and outline of the proof with emphasis on heuristics of main features, such as the long- range interaction between blow up profile and asymptotic profile $z$, and rotational instability mechanism. See the video of the talk
on our YouTube Channel.
|

Dan Parman
Endowed Distinguished Professor @University of Texas at San Antonion
Professor Gui received his Ph.D. from University of
Minnesota (United States), he held positions @University of
British Columbia, Vancouver (Canada) and @University of
Connecticut. Professor Gui was a Simons Fellow in 2019 and a
Fellow @American Mathematical Society in 2013.
|
AbstractThe classical Moser-Trudinger inequality is a borderline case of Soblolev inequalities and has important applications in geometric analysis and PDEs. On the two dimensional sphere, Aubin in 1979 showed that the best constant in the Moser-Trudinger inequality can be reduced by half if the functions are restricted to a subset of the Sobolev space $H^1$ with mass center of the functions at the origin, while Onofri in 1982 discovered an elegant optimal form of Moser-Trudinger inequality. In this talk, I will present new sharp inequalities which are variants of Aubin and Onofri inequalities on the sphere with or without constraints. One such inequality, for example, incorporates the mass center deviation (from the origin) into the optimal inequality of Onofri on the sphere. In another view point, this inequality also generalizes to the sphere the Lebedev-Milin inequality and the second inequality in the Szegö limit theorem on the Toeplitz determinants on the circle, which is useful in the study of isospectral compactness for metrics defined on compact surfaces, among other applications. The talk is based on a joint work with Amir Moradifam (University of California, Riverside) and a recent joint work with Alice Chang (Princeton). Video recording to the talk |

Professor @Waseda University
Funaki was a Professor @The University of Tokyo from 1995 until
2017 and is now a Professor @Waseda University from
2017. He is a Professor Emeritus of the University of Tokyo.
|
AbstractIt's one of common interests in probability group to derive nonlinear PDEs or stochastic PDEs from microscopic interacting systems via scaling limits in space and time, usually by some averaging effect caused by the local ergodic property of the microscopic systems. In the talk, we discuss the derivation of two objects: Motion by mean curvature (MMC) and coupled KPZ (Kardar-Parisi-Zhang) equation. The microscopic system we take is that of particles which perform random walks with interaction. To derive MMC, we allow creation and annihilation of particles. The system exhibits a phase separation to sparse and dense regions of particles and, macroscopically, the interface separating these two regions evolves under the MMC. We pass through the Allen-Cahn equation with nonlinear Laplacian at an intermediate level. On the other hand, the coupled KPZ equation is a system of nonlinear singular stochastic PDEs. It is ill-posed in a classical sense and requires renormalizations. We derive it under the fluctuation limit of multi-species weakly-asymmetric particle system of interacting random walks without creation and annihilation. The so-called Boltzmann-Gibbs principle plays a fundamental role for both. References
The first part is joint work with S. Sethuraman, D. Hilhorst, P. El Kettani and H. Park ( arXiv:2004.05276), while the second is with C. Bernardin and S. Sethuraman ( arXiv:1908.07863). Video recording to the talk |

Research Fellow
@Tsuda University (Japan), Professor Emeritus @Waseda University
(Japan), Fellow @American Mathematical Society
Professor Ishii received his Ph.D. from Waseda University in June
1975. He worked at Chuo University from 1976 until 1996, at
Metropolitan University from 1996 until 2001, and at Waseda University from 2001 until 2018.
|
Abstract
In the talk, I discuss the recent developments of the vanishing
discount problem. The main focus concerns that for monotone
systems of Hamilton-Jacobi equations. The principal tool in the
analysis for the vanishing discount is the use of Mather
measures from Aubry-Mather theory or their generalizations. I
explain a way of constructing Mather measures and an approach
to the vanishing discount problem.
This talk bases on joint work with Liang Jin of Nanjing University of Science and Technology. References
Video recording to the talk |

Professor
@ Xiamen
University, China
Professor Xia received his PhD in July 2012 from the Albert Ludwig University of Freiburg in Germany. He was a doctoral student of Professor Guofang Wang. Professor Xia was a Postdoc Fellow at the Max Planck Institute for Mathematics and Sciences at Leipzig in Germany from 2012-2014, and Postdoc Fellow at McGill University in Montreal, Canada, from 2015-2016.
|
AbstractLichnerowicz-Obata's theorem says that for a closed $n$-manifold with Ricci curvature $Ric\ge (n-1)K>0$, the first (nonzero) eigenvalue is greater than or equal to $nK$, with equality holding only on a round $n$-sphere. Similar results for the first Dirichlet eigenvalue and Neumann eigenvalue have been shown by Reilly, Escobar and C.Y.Xia respectively. For the first (nonzero) Steklov eigenvalue, a conjecture has been made by Escobar saying that for a compact manifold with boundary which has nonnegative Ricci curvature and boundary principal curvatures bounded below by some $c>0$, the first (nonzero) Steklov eigenvalue is greater than or equal to $c$, with equality holding only on a Euclidean ball. This conjecture is true in two dimensions due to Payne and Escobar. In this talk, we present a resolution to this conjecture in the case of nonnegative sectional curvature in any dimensions. We will also discuss a sharp comparison result between the first (nonzero) Steklov eigenvalue and the boundary first eigenvalue. This is a joint work with Changwei Xiong. Video recording to the talk |